【Database】性能调优学习笔记(4)- 索引(2)
上一篇文章记录了一下解析了一下索引,索引的种类。本质上索引其实是一种数据结构,并且放在硬盘上。通常MySQL中索引使用的数据结构是B+树,下面再进行相关的记录解析。
应用服务一般都是放在服务器上跑,那么必然存在着磁盘和内存两种存储介质。
一般来说,内存都是作为临时存放的介质存放数据,不能进行持久化,遇到意外比如服务器宕机重启的时候,在内存里的数据就会丢失。而磁盘上在不手动删除或者磁盘出现问题的前提下,数据将被永久的存储,这就是为什么索引要存储在磁盘上的原因。
尽管通过索引来多次查询数据的时候,在内存读取数据比起在磁盘进行I/O操作消耗的时间更短,但毕竟这是长时间使用的内容,不能因为一些意外情况就让索引丢失。
索引使用的数据结构是树,那么如果使用二叉树/平衡二叉树(如:红黑树)等作为索引的结构的话,数据量越大,树的高度越高,那么需要进行的磁盘I/O操作越多,自然查询的效率就越低。故而就有了B树以及B+树的出现。
B树(Balance Tree)-> 多路平衡查找树的解析
在解析B树之前先了解下相关的名词、特性:
阶:B树的每一个节点可以包含M个子节点,M就称为B树的阶。
一个M阶(M > 2)的B树有以下特性:
- 根节点的儿子数范围为[2, M]。
- 非叶子节点有K-1个关键字,K个孩子,K的取值范围为[ceil(M/2), M]。
- 叶子节点有K-1个关键字,无孩子,K的取值范围为[ceil(M/2), M]。
- 非叶子节点的关键字:K[1]、K[2]…K[k-1],从小到大的顺序排列即K[i] < K[k+1]。
- 非叶子节点的指针:P[1]、P[1]…P[k],由于K-1个关键字相当于划分了K个范围,所以
(1)、P[1]指向了关键字小于K[1]的子树;
(2)、P[i]指向了关键字属于(K[i-1], K[i]);
(3)、P[k]指向了关键字大于K[k-1]的子树;
针对第5点,如下图所示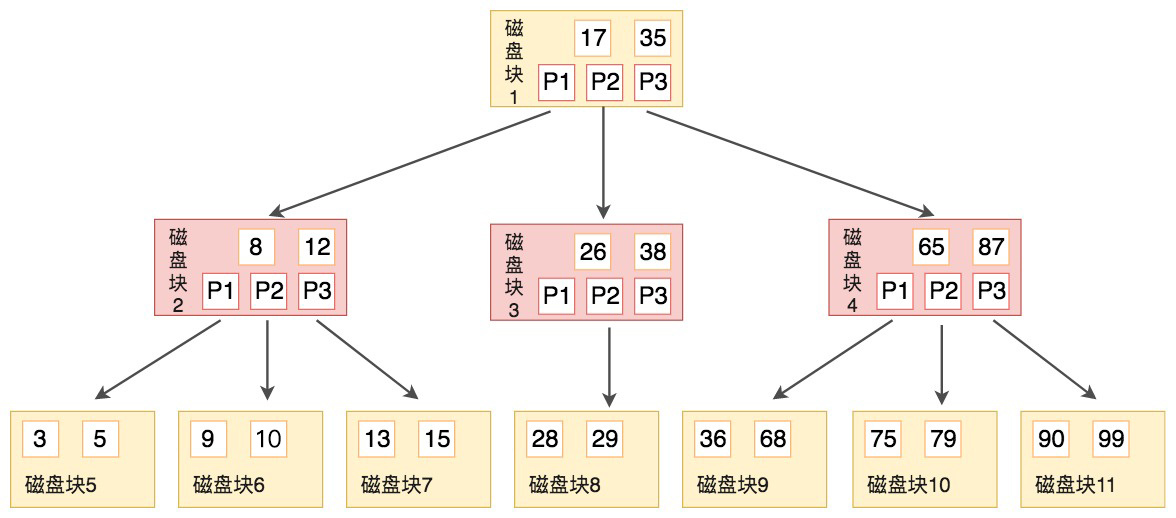
附上一个可以在线可视化操作的地址 - 所有的叶子节点位于同一层。
通过B树来进行查询就是通过上述第5点的方式来找到指针,最后确定结果的所在。在此过程中比较的次数其实并不少,但因为数据是读取出来放到内存里比较的话,这个时间就会非常的短。所以这里的重点是磁盘的I/O操作的次数,因为B树的节点中能存多个元素,所以磁盘的I/O操作会比较少,而二叉树每个节点只能有一个元素,所以在查询中B树比平衡二叉树的效率要高。
B+树
B+树是在B树的基础上做出了改进,B+树和B树的差异是:
- 在B+树中,孩子数量 = 关键字数量。在B树中,孩子数量 = 关键字数量 + 1。
- 非叶子节点的关键字也会存在子节点中。
- 在B+树中,非叶子节点仅用于索引,其关键字不保存数据,所有数据都保存在叶子节点。在B树中,非叶子节点既保存索引,也保存数据。
- 所有关键字都会在对应的叶子节点上出现,并且形成一个有序链表,从小到大按顺序链接。
下图是一颗B+树: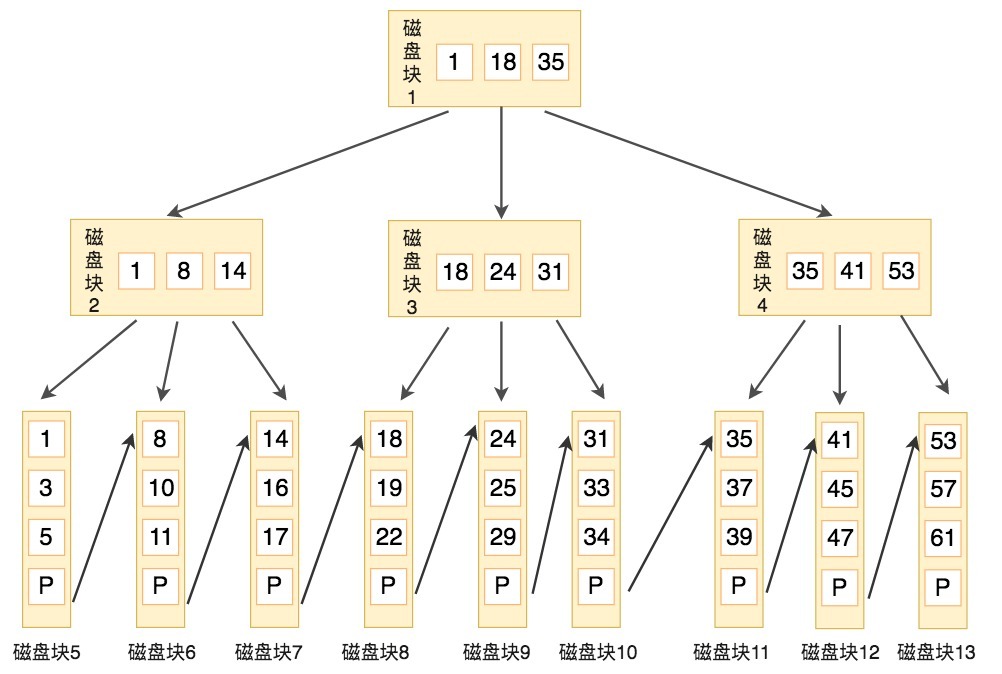
可以看到,从根节点开始,每一个节点都会存储父节点对应的关键字,并且从小到大形成有序链表。
本质上,B+树和B树的查询过程差不多,主要的差别还是在非叶子节点不存储数据上。这样的好处是:
- B+树查询的效率更加稳定。
这里主要体现在,B+树每次查询,最终只能在叶子节点上获取到数据。但是B树的话,有可能在叶子节点上获取到,也有可能在非叶子节点上获取到。 - B+树查询的效率更高。
这是因为通常B+树会更矮更胖(阶数更大,深度更低),主要是B+树单一节点可以存更多的关键字,因此I/O操作更少,效率更高。并且所有的叶子节点形成了一个有序链表,更便于查找。
学习参考来自课程《SQL必知必会》
